728x90
풀이 방법
매번 느끼는건데 백준에서의 수학 관련된 문제들은 옳곧이 수학적인 계산을 하는 것보다는 일종의 '꼼수'를 발견하는게 중요하다고 느낀다.
저번 A->B 문제도 그렇고, 이 문제도 그렇다. 오히려 수학 계산을 정말 하면 시간초과가 터지는 그런...?
사실 문제를 계산한다 라는 느낌보다는 '순수익이 어떻게 기준점을 넘길까?' 를 생각해보면 쉬워지는 문제이다.
예컨데 순수익을 먼저 계산한 후 순수익을 기준으로 고정비용을 몇일만에 넘길 수 있는가? 를 생각하면 되는 문제이다.
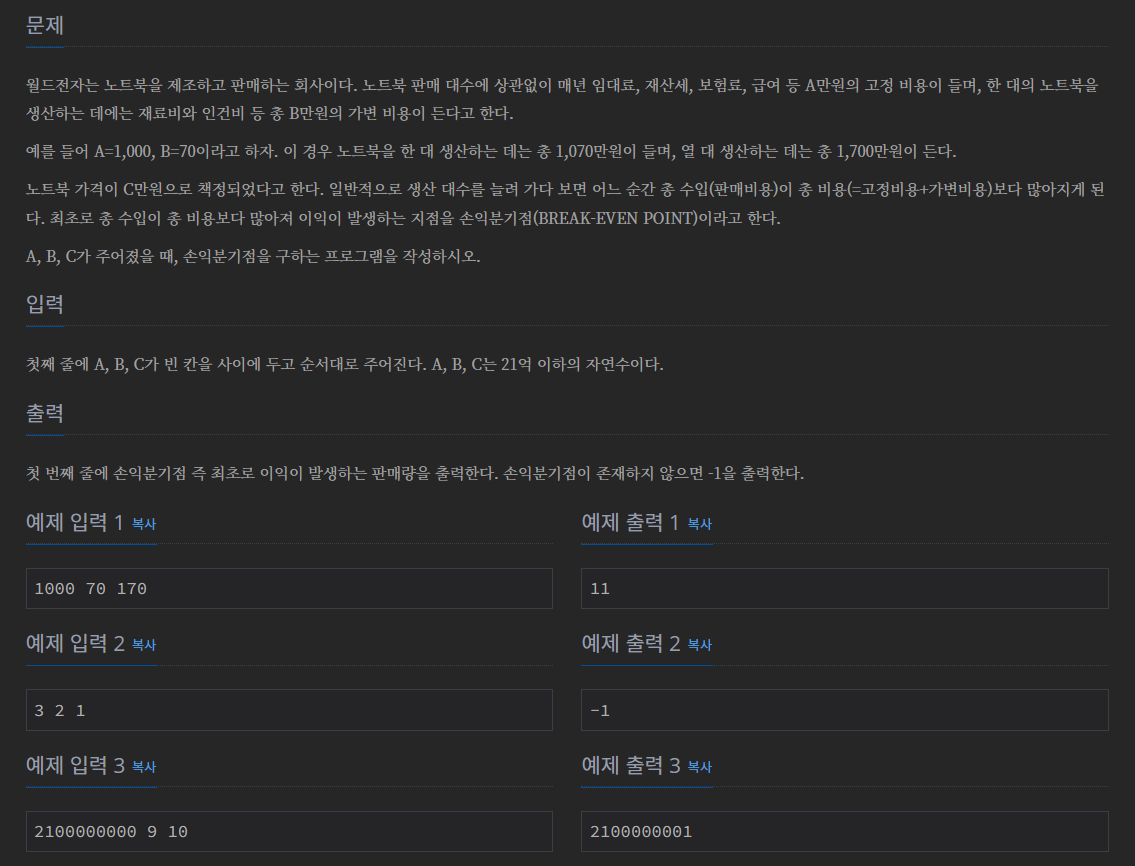
A = 1000, B = 70, C = 170 인 경우
1일차 : 1000+70*1 , 170*1 을 비교
2일차 : 1000+70*2 , 170*2 을 비교
n일차 : 1000+70*n , 170*n 을 비교
이때 고정비용인 A 를 빼놓고 가변비용인 70 과 판매액인 170 을 비교해서 생각하자하면 하루 순수익은 100 이 된다. 따라서 순수익이 고정금액을 넘을 수 있는 최소 일수를 계산해주면된다.
즉 170 - 70 을 한 순수익을 계산한 뒤, 순수이이 고정비용을 넘어야함으로 고정비용을 순수익으로 나눈 값 +1 하면 손익분기점을 넘는 최소 일수가 계산된다.
나머지는 주석 참고!!
package baekJoon;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
// 수학 문제들은 정상적으로 계산할 생각 말자
// 정공법 풀이보다는 어떻게든 쉬운 방법 -> 꼼수를 찾자
public class Quiz_1712 {
// 21억이하의 자연수 임으로 int 대신 long 으로 받음
static long a,b,c;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
a = Long.parseLong(st.nextToken());
b = Long.parseLong(st.nextToken());
c = Long.parseLong(st.nextToken());
long result = breakEventPoint();
System.out.println(result);
}
// A = 1000, B = 70, C = 170 인 경우
// 1일차 : 1000+70*1 , 170*1 을 비교
// 2일차 : 1000+70*2 , 170*2 을 비교
// n일차 : 1000+70*n , 170*n 을 비교
// 이렇게 되는데 쉽게 생각하자면 고정비용인 A 를 빼놓고
// 가변비용인 70 과 판매액인 170 을 비교해서 생각하자하면 하루 순수익은 100 이 된다.
// 따라서 순수익이 고정금액을 넘을 수 있는 최소 일수를 계산해주면된다.
// 즉 170 - 70 을 한 뒤, 고정비용을 순수익으로 나눈 값 +1 하면 손익분기점을 넘는 최소 일수가 계산된다.
static long breakEventPoint(){
long n = c - b;
long m = 0;
if (n <= 0) {
return -1;
}
m = a/n;
return m+1;
}
}
'Java - 알고리즘' 카테고리의 다른 글
| 백준 - 1647 도시 분할 계획 (0) | 2022.08.27 |
|---|---|
| 백준 - 1922 네트워크 연결(feat. 크루스칼 알고리즘) (0) | 2022.08.24 |
| 백준 - 5397 키로거 (0) | 2022.08.22 |
| 백준 - 2798 블랙잭 (0) | 2022.08.21 |
| 백준 - 11652 카드 (0) | 2022.08.20 |


댓글