728x90
데이크르스라 알고리즘 Dijkstra Algorithm
일명 다익스트라 알고리즘이라고도 한다.
- 보통 음의 가중치가 없는 가주치 방향 그래프를 기준으로 최소 비용으로 노드를 방문하거나 노드를 이어가는 문제들에 많이 쓰인다 => 가중치 방향 그래프란 노드에서 다른 노드로 갈 때 일정한 비용이 드는 그래프를 의미한다.
- 기본적으로 O(V^2) 의 시간복잡도를 가지나 PriorityQueue 나 sort 를 사용해서 O(VlogV) 의 시간 복잡도를 만들어서 계산하게 된다.
다익스트라 알고리즘 코드
보통 아래와 같은 순서로 코드 작성한다.
0. 정점과 비용을 위한 Edge class 를 만들어둔다
1. n번째 노드에서의 최소 cost 로 방문할 수 있는 도로를 찾기위해 PriorityQueue 를 사용한다.
2. n번째 노드와 연결되는 노드를 표시하기 위한 ArrayList 를 만든다 => ArrayList.add(ArrayList<Edge>)
3. n번째 노드와 연결되는 노드 a 및 비용 b 을 ArrayList 에 담는다. => ArrayList.get(n).add(new Edge(a, b))
4. 각 노드까지의 비용을 저장하기 위한 dis 배열 생성
5. 계산하기!! => solution 주석 참고
다익스트라 알고리즘 문제 풀기
첫째줄에 노드의 갯수 n 과 간선의 수 m 이 주어진다.
다음줄부터 m+1 번째줄까지 노드와 연결된 노드, 해당 노드까지의 비용이 주어진다.
이때 각 노드를 방문하는 최소 비용을 출력해보자
단, 노드에 방문할 수 없는 경우 도착 불가로 표시하자
입력
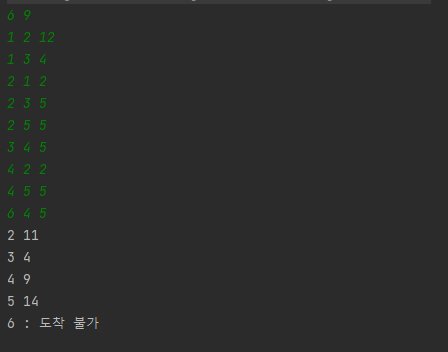
6 9
1 2 12
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5

package algorithm;
// 데이크스트라 : 다익스트라 알고리즘
// 보통 가중치 방향 그래프와 최소 비용으로 방문하는 문제들에 많이 쓰인다.
// 가중치 방향 그래프란 노드에서 다른 노드로 갈 때 일정한 비용이 드는 그래프를 의미한다.
// 도시와 도시를 잇는 도로와 해당 도로의 유지비를 생각하자
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
// 다익스트라 알고리즘을 코드 짜기
// 0. 정점과 비용을 위한 Edge class 를 만들어둔다
// 1. n번째 노드에서의 최소 cost 로 방문할 수 있는 도로를 찾기위해 PriorityQueue 를 사용한다.
// 2. n번째 노드와 연결되는 노드를 표시하기 위한 ArrayList 를 만든다 => ArrayList.add(ArrayList<Edge>)
// 3. n번째 노드와 연결되는 노드 a 및 비용 b 을 ArrayList 에 담는다. => ArrayList.get(n).add(new Edge(a, b))
// 4. 각 노드까지의 비용을 저장하기 위한 dis 배열 생성
// 5. 계산하기!! => solution 주석 참고
/*
*
6 9
1 2 12
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
*
* */
public class Algo_Dijkstra {
static ArrayList<ArrayList<Edge>> graph = new ArrayList<ArrayList<Edge>>();
static PriorityQueue<Edge> q = new PriorityQueue<Edge>((o1, o2) -> {
return o1.cost - o2.cost;
});
static int[] dis; // 해당 노드까지의 비용을 저장하기 위한 dis 배열
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
// 거리 배열 초기화
// 0 이 아닌 1번 노드 부터 시작함으로 n+1
dis = new int[n + 1];
// 각 노드까지의 최소 비용을 넣어야함으로 최대값으로 초기화
Arrays.fill(dis, Integer.MAX_VALUE);
for (int i = 0; i < m; i ++) {
int a = scan.nextInt();
int b = scan.nextInt();
int c = scan.nextInt();
// a 번째 노드와 이어진 b 번째 노드, b 노드까지의 비용
graph.get(a).add(new Edge(b, c));
}
// 시작하는 노드를 메서드에 넣는다.
solution(1);
for(int i=2; i<=n; i++){
if(dis[i] != Integer.MAX_VALUE) System.out.println(i + " " + dis[i]);
else{
System.out.println(i+" : 도착 불가");
}
}
}
static void solution(int v){
q.offer(new Edge(v , 0) );
dis[v] = 0;
// queue 가 빌때까지 계속 반복
while (!q.isEmpty()) {
// q 하나만 빼서 Edge 객체를 각각 nowNode, nowCost 에 저장
Edge node = q.poll();
int nowNode = node.vex;
int nowCost = node.cost;
// nowCost 가 dis[nowNode] 보다 크다면 continue;
// 해당 if 문은 이미 dis[nowNode] 에 방문한 경우 이에 대해 체크하기 위해서이다.
// 즉 dis[nowNode] 의 값보다 queue 에서 나온 nowCost 의 값이 큰 경우
// nowNode 에 도착하기 까지 더 많은 비용이 드는 방법임으로 해당 방법으로는 갈 필요가 없다.
// 즉 비용이 더 많이 드는 방법으로 노드를 탐색할 필요가 없기 때문에 무시하고 continue 한다.
if (nowCost > dis[nowNode]) {
continue;
}
// graph 를 이용해 현재 nowNode 와 연결된 Edge 를 가져와서 for 문을 돌린다.
for (Edge next : graph.get(nowNode)) {
// 이때 다음 노드까지의 비용 - dis[next.vex] - 이
// 현재 노드까지의 비용+다음 노드까지의 비용 보다 작다면
if (dis[next.vex] > nowCost + next.cost) {
// 다음 노드까지의 비용을 현재 노드까지의 비용 + 다음 노드까지의 비용 으로 변경 => 노드 방문 완료
dis[next.vex] = nowCost + next.cost;
// 다음 노드에 방문했음으로 queue 에 해당 노드와 해당 노드까지의 비용을 넣고 끝!
q.offer(new Edge(next.vex, nowCost + next.cost));
}
}
}
}
}
class Edge{
int vex;
int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
}
결과
- Reference
유튭 강의 : EBS
https://www.youtube.com/watch?v=tZu4x5825LI&t=2s
https://m.blog.naver.com/ndb796/221234424646
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐...
blog.naver.com
[알고리즘] 다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘과 구현 방식, 예시 문제
velog.io
'Java - 알고리즘' 카테고리의 다른 글
| 백준 1193 : 분수찾기 (0) | 2022.08.30 |
|---|---|
| 백준 - 2839 설탕배달 (0) | 2022.08.29 |
| 백준 - 1647 도시 분할 계획 (0) | 2022.08.27 |
| 백준 - 1922 네트워크 연결(feat. 크루스칼 알고리즘) (0) | 2022.08.24 |
| 백준 - 1712 손익분기점 (0) | 2022.08.23 |


댓글